How a Little Money Can Turn into a Lot
Welcome to class! If you were to only master one topic in your time here, I hope it is this one. Compounding is truly the basis of all investing. It is what makes charts like the one below possible. Let’s see how it happens.
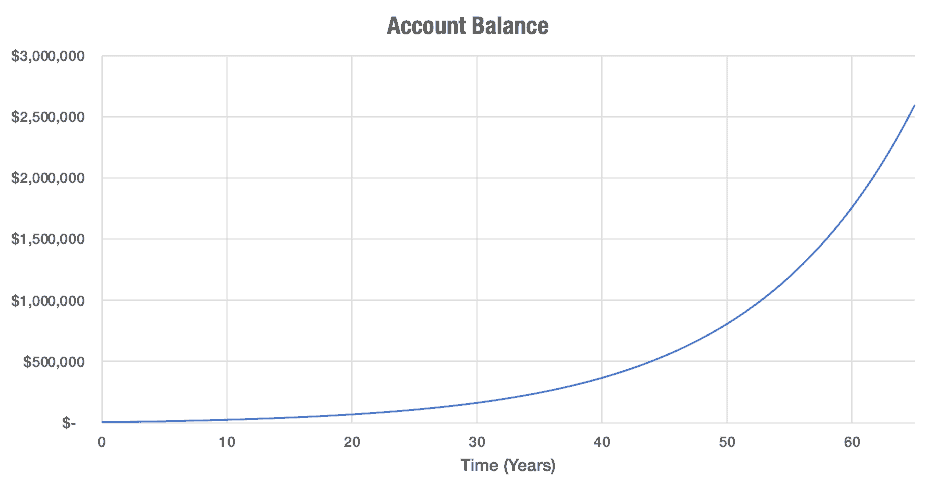
As a saver and investor, the upward sloping curve is where it feels like magic happens. It’s not just a straight line, moving up and to the right at a constant rate. It grows faster-and-faster… the balance grows itself! Just by sitting there until you need it. The magic that happens is described by a short bit of math.
Future Value = Current Value*(1+Growth Rate)^{Time}If you want to know what that looks like in a math nerd’s brain or a business school textbook, it would be this
V_F = V_C*(1+R_g)^t
Why does the line of value follow a curved trajectory rather than just a straight line? Because of that exponent (time). Exponential growth is powerful!
Let’s look at where the term compounding takes shape. The word compound as a noun means one thing that is made up of two other things. A compound word, like paycheck, is made up of the word pay and the word check. When combined it gives a new – and I would argue more important – meaning.
When used as a verb it can describe putting separate things together. When a chemist mixes two substances together to make a third, they are said to be compounding. They are making a new substance from two other substances.
A bone with more than one break is said to have suffered a compound fracture. Compound fracture seems to be a compound term to describe something that has undergone compounding.
Let’s look at how compounding affects your investments. Pretend that I give you $1,000. I like you because you seem responsible, so it seems worth it. You, being a responsible individual, decide to invest the $1000 in an investment that will return you 8% per year for the life of the investment. I emphasize per year here for a reason. Those two words are what describes the ability to grow invested money exponentially with time. Remember that little formula from above? No, okay, here it is again.
Future Value = Current Value*(1+Growth Rate)^{Time}If you start off with $1,000 (current value) and it grows 8% (8% = 0.08) during the first year (time = 1), at the end of the year you have $1,080. $80 more than you started the year with.
V_F(t=1)= \$1000*(1+.08)^{1}=\$1080The second year if I earn 8% again, I end up with $1,166.40.
V_F(t=2)= \$1080*(1+.08)
-or-
V_F(t=2)= \$1000*(1+.08)^{2}The second year of growing at the same rate, yielded a profit of $86.40 for the year. This is more than the first year. How? What I earned in growth the previous year, becomes part of what is growing (the principle). This becomes a new thing, as we discussed before. Now this new balance grows the second year at the per year rate. This is how compounding happens. Each year of growth ends up yielding more in returns than the year before [1].
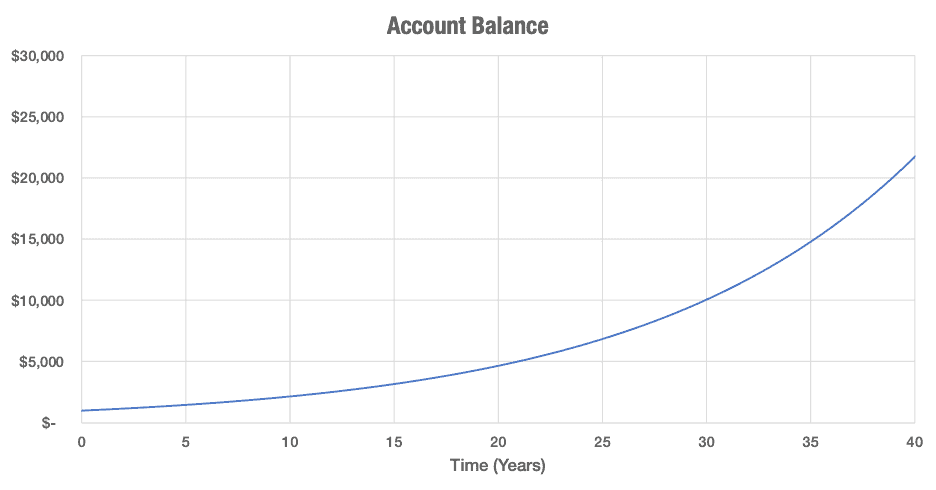
Let’s jump forward in time to year ten. After nine years of compound growth at 8%, your original $1,000 becomes $1,999.00. In the tenth year, your value grows to $2,158.93, with an annual profit of $159.92, basically double what your profit was year one.
In year forty, the numbers get even more fun. Your original $1,000 starts the year being worth $20,115.29 and earns $1,609.23 during the year to bring the value at the end of year forty to $21,724.52.
Here is what your $1,000 looks like over time with the magic of compounding.
A Use Case of Compounding
To help crystalize this, let’s look at a specific use case. Often times, we are limited by our imagination in thinking out many years. When we are talking about saving and investing for the future, our time horizons can go past our own lives. Imagine two parents having a child this year. To get them started off right, they put away $5,000 in an account for their newborn. Appropriately managed, it is not unreasonable to expect to earn 8% interest. The S&P 500 index, for example, has averaged just under 12% annual returns since its inception in 1957.
Growing at 8% a year, that $5,000 would grow to over $230,000 when they turn 50 and over $740,000 when they turn 65. That’s a pretty great start the parents have provided the new love of their life!

Okay, but how do you get to that first chart we looked at, the one that makes you a millionaire? If $1,000 was added to the account every year, the numbers jump to over $800,000 at age 50 and over $2,500,000 by age 65.

It really is worth holding on to some of what you earn and putting it away for the future.
Notes:
[1] This is assuming a constant growth rate, which is sometimes-but-definitely-not-always the case. We’ll get to the more complex cases in the future. To begin understanding the basic principle, think about a simple application first.